1. 들어가기 전에
어떤 파도타기를 좋아하는 사람이 있다고 합시다. 보통의 파도는 너무도 잘 타지만 이 사람은 한계가 어디까지인지 궁금했습니다. 문제는 파도의 높이와 바람의 방향에 따라 잘못하면 파도를 타다가 죽을 수도 있다는 거겠죠. 파도가 아무리 높아도 바람이 세지 않다면 별 문제가 없을 거고요. 바람의 방향도 자신의 방향인지 반대 방향인지에 따라 파도의 높이가 문제가 안될 수도 생명이 위태로울 수도 있는 거죠. 바람의 방향이 내륙 쪽이고 파도가 높다면 즉시 파도타기를 중지하고 휴식을 취해야 하지만 파도가 높고 바람의 방향이 바다를 향한다면 그것은 서퍼에게는 최고의 도전이 되겠죠. 눈치 채셨나요? 요즘 Bitcoin 시장이 위의 내용과 비슷합니다. 일주일 단위로 급등락을 하고 있습니다. 보통 주말을 주기로 급락을 하고 주 후반에 급등을 했다가 또 어느샌가 급락을 합니다. 폭은 대략 이더리움 기준으로 약 40만 원 선을 왔다 갔다 하지만 어느새 이더리움 가격은 최고점 대비 반토막이 났고 비트코인도 맞찬가지 입니다. 현재 시점 기준 비트코인은 반등했지만 4천이 안 되는 선에서 박스권을 만들고 있습니다. 다시 파도타기 이야기로 돌아간다면 바람의 방향이 언제 바뀔지 파도의 세기는 얼마나 되는지(바람의 세기와 비례하겠죠?) 파도의 높이는 어느 정도 되는지 (미리 예측하는 것이 아니라) 현시점의 변화만 알아도 얼마든지 파도타기에 도전하는 것은 무리가 없겠죠? 다시 비트코인 세계로 돌아온다면 이 모든 것을 결정하는 것은 무엇일까요? 사람들은 이동평균선으로 대충의 추세를 예측하지만 컴퓨터(프로그램)는 불행히도 인간이 보는 이동평균선을 볼 수 없습니다. 대신에 점으로 보는 거죠. 근데 문제는 점으로는 앞의 추세를 판단할 수가 없습니다. 여기서 미적분이 필요합니다. 문과분이나 수학을 잘하지 못했던 분들은 미적분이라는 소리에도 놀라시겠지만 제가 하려는 미적분은 실제로는 미적분과 거리가 멀다고 할 수 있습니다. 그냥 대충의 미적분인 것입니다. 왜냐하면 컴퓨터는 0 또는 1만 이해할 수 있고 프로그램에서는 true와 false만 이해를 할 수 있으므로 그에 대입되는 값의 정확도는 그리 중요하지 않습니다.
2. 자동매매 분석에 미적분이 필요한 이유
먼저 미분에 대하여 여러분은 예전 고등학교 시절 무엇이라고 기억하고 계신가요? 왜 미분을 해야 하는지에 대한 내용이나 미분을 하는 방법에 대하여 배우신적이 있으신가요? 지금 우리가 하려는 미분은 이전 수학 시간에 배우던 그런 어려운 미분이 아닙니다. 인간은 모든 데이터 및 주위 환경을 이해하기 위해서 아날로그 데이터를 사용합니다. 이전에는 모니터도 아날로그 음악도 아날로그 모든 것이 아날로그였지만 현재는 모든 것이 디지털입니다. 그럼 여러분 아날로그와 디지털의 차이는 무엇일까요? 예로 제가 처음 컴퓨터 프로그래머로 일했을 때 제가 주로 했던 일이 콜센터의 지능형 ARS 즉 IVR이라는 시스템을 설치하고 프로그래밍하는 일이었습니다. 이때 아날로그인 음성을 디지털로 만드는 것을 샘플링이라고 하고 주로 1초에 8000번 샘플링한 데이터를 사용하여 프로그래밍 해었습니다. 하지만 아날로그의 절대 끝은 존재하지 않아서 인간의 가청 주파수인 20000Hz 이상의 데이터는 버리고 샘플 했습니다. 즉 주변의 소리도 1초에 8000번만 높이를 기록하면 다시 소리로 변환할 때는 정상 소리와 구분이 안 가고 사람이 알아들을 수 있습니다. 요즘은 음악 녹음할 때는 198000번 정도의 초당 샘플링을 합니다. 그러면 사람은 거의 원본 녹음과 디지털 음을 구분하지 못합니다.
다시 비트코인의 세계로 돌아 와서 우리 사람은 쉽게 이해할 수 있는 이동평균선(MA)을 컴퓨터(프로그램)가 이해하고 학습할 수 있게 할 수 있을 까요? 위 이야기의 파도타기처럼 컴퓨터가 어떤 이동평균선이 위험한지 어떤 게 안전한지 폭락 후 멈출 때 현상은 무엇인지 폭등이 시작된 것은 어떻게 판단할지 폭등은 언제쯤 멈출 것이며 폭등 후의 행동은 무엇일지 컴퓨터가 판단할 수 있는지에 대한 이야기입니다.
다시 저의 초기 프로그래머 시절로 돌아가서 소리를 8000번 샘플링하는 것을 PCM(Pulse-code modulation)이라고 했습니다. 여기서 중요한 것은 8000번 샘플링에는 일정한 주기가 있다는 것 입니다. 컴퓨터가 우리가 사는 3차원의 세계를 이해하려면 자신이 있는 1차원의 세계의 데이터로 변환하는 일이 필요합니다. 혹시 Deep learning공부를 하신 분들이 계신가요? 딮러닝 공부를 하신다면 무슨 게이트 무슨 게이트 시그모이드니 뭐니 하는 것들을 가만히 생각해 보시면 결국 다차원의 데이터를 1차원의 데이터로 변환하는 가정이라는 것을 아시게 되실 겁니다. 결국은 컴퓨터는 1차원 데이터 외에는 이해 불가라는 거죠. 다시 고등학교 시절로 돌아가서 미분을 다시 배운다면 미분은 다차원의 데이터를 1차원 데이터로 변환하는 가정이라고 배우신다면 좋을 듯합니다.(왜 그때는 수학을 어렵게만 가르쳤는지 저는 이해가 잘 안 됩니다.) 이게 뭔 말이냐 하면 우리가 분석하려는 이동평균선은 고차원 방정식의 곡선입니다. 변화무상하고 매 순간 변화하지만 일 순간은 점(dot)이라는 사실이죠. 이 점(dot)은 바로 컴퓨터가 이해할 수 있는 1차원 데이터 입니다만 문제는 이 점(dot)이 완벽한 데이터가 되려면 방향이 필요합니다. 그래서 제가 생각한 게 바로 각도입니다. 곡선의 한 점을 미분하면 그 지점의 각도를 구할 수 있습니다. 혹시라도 고등학교 수학을 놓치지 않으셨다면 다들 알고 있는 것일 겁니다.

간단하게 미분식을 표현한다면 앞의 식처럼 표현 하겠지만 정식적인 표현은 'f(x) = 기울기*x + 절편' 이런 식의 식이 나올 겁니다. 하지만 우리가 필요한 것은 기울기만 필요합니다. 시간 단위로 움직이는 평균 이동선의 값의 변화는 pandas를 이용하면 아주 쉽게 구할 수 있습니다. pandas DataFrame을 df라고 하고 평균 이동선을 sma120(120개 이동평균선)이라고 하면 dy = df.sma120 - df.sma120.shift()로 쉽게 구할 수 있습니다. 그렇지만 시간의 변화 값을 구하는 것은 실제로는 불가능합니다. 하지만 상관없습니다. 우리는 대충의 근접 치를 구하는 것이지 딱 이 값 이런 식의 값을 구하는 것이 아닙니다. 우리는 컴퓨터 프로그램에서 사용할 수 있는 오차가 있어도 다른 값과 커플링 되지 않으면서 비교가 가능하고 방향성을 가지는 값만 구하면 됩니다. 그래서 저는 dt값을 대충 3*60 정도로 하기로 했습니다. <제가 살다 보니 사람들 마다 문과 머리와 이과 머리가 따로 있는 것 같더군요. 제가 위처럼 dt를 대충 3*60이라고 정한다고 하면 이과 머리는 절대로 이해를 못합니다. 근데 수학을 잘 못하는 문과생들은 "그래"하고 금방 수긍하죠.> 그 다음 다시 수학입니다. 그냥 인터넷만 뒤지면 나오는 기울기로 각도 구하는 공식입니다. python으로 식을 구하면
df['sma120_inc'] = df.sma120 - df.sma120.shift()
df['sma120_radians'] = df['sma120_inc'].apply(lamda x: math.atan2(x, 3*60))위와 같이 될 겁니다. 그럼 sma120_radians는 -π/2 ~ π/2 를 리턴할 겁니다. 이 값보다는 -90 º ~ 90 º 표현되는 값이 훨씬 이해하기가 쉬울 겁니다. 그래서 다시 python 식을 바꾸면
df['sma120_incli'] = df.sma120 - df.sma120.shift()
df['sma120_degrees'] = df['sma120_incli'].apply(lambda x: math.degrees(math.atan2(x, 3*60)))위와 같이 표현이 됩니다.
2장에 나오는 class Auxiliary 에 위 부분을 추가하면 이제는 각 보조 지표들에 대하여 하락 중인지 상승 중인지를 알 수 있습니다. 저 같은 경우는 이 블로그 초기에 5분 데이터를 버리고 지금은 1분 데이터를 사용하고 있으며 1200분의 이동평균선(이하 sma1200)을 주로 이용하고 있고 이 값은 현재 급변하는 비트코인 시장에 너무나도 잘 맞고 있습니다. 신기할 정도입니다. sma1200의 각도인 sma1200_degrees는 위의 식을 잘 응용하신다면 쉽게 구하셨을 거라고 생각합니다. 그리고 제 프로그램에 위의 식을 이용하여 sma1200_degrees가 30 º 를 초과하면 급등 구간으로 정의하고 40 º 를 초과하면 급급등 구간으로 정의했습니다. 그래서 30 º초과하는 경우 조건식이 뭐건 상관없이 무조건 매수하게 했습니다. 40 º 를 초과하면 절대로 매도를 안 하는 거죠. 왜냐면 계속 오를 테니까요? 하지만 여기에는 문제가 있습니다. 우리가 파도를 타는 사람이라고 생각하면 무엇보다도 바람의 방향이 중요합니다. 바람의 방향을 무시하면 생명과 직결되는 문제가 발생합니다. 바람의 방향이 바뀌면 바로 모든 것을 버리고 해변으로 나와야 하죠. 순풍이라고 신이 나서 죽음이 다가오고 있는지 모르고 즐기고 있다면 죽음의 신이 바로 옆에 있는데 춤을 추는 꼴이겠죠. 그래서 제가 생각한 값이 곡선의 밑면과 닫는 넓이입니다. 밑변은 840분 동안의 최저가를 사용했습니다. 그리고 우리는 위의 각도를 알고 있기 때문에 곡선에서 90 º로 내린 선과 곡선의 기울기를 이용한 각도인 sma1200_degrees와 840분 동안의 최저가를 이용하면 하나의 직각 삼각형을 구할 수 있다는 것을 쉽게 이해하실 겁니다.
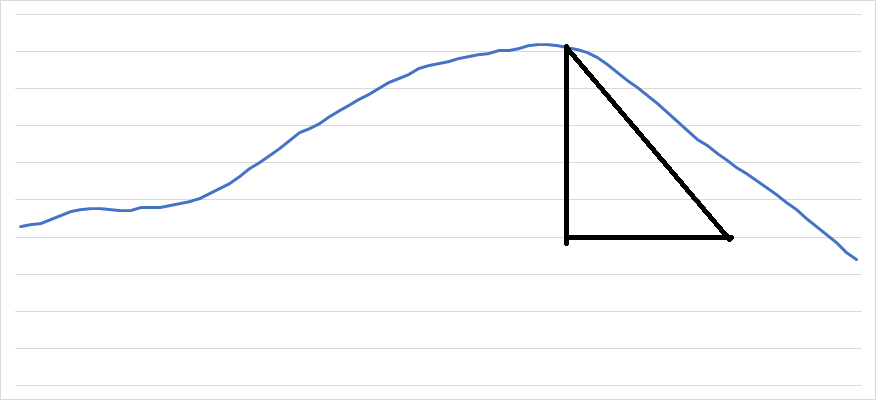
대충 옆의 그림처럼요 이 삼각형의 넓이를 대충 저는 minus_range라고 정했습니다. 이 값은 굉장히 큰값이 나옵니다. 이 값을 이용하면 파도의 힘과 방향을 알 수 있지만 역시나 값이 너무 큽니다. 그래서 다시 한번 이 값의 이동평균선을 구했습니다. 왜냐하면 이제는 어떤 이동평균선이 와도 컴퓨터(프로그램)는 이해할 수 있기 때문이지죠 아래 python코드를 보시면 아실 겁니다.
df['sma1200'] = talib.SMA(np.asarray(df['close']), 1200)
df['sma1200_incli'] = df.sma1200 - df.sma1200.shift()
df['sma1200_degrees'] = df['sma1200_incli'].apply(lambda x: math.degrees(math.atan2(x, 3*60)))
df['sma1200_minus_range'] = df.apply(lambda x: 0.5* ((x['sma1200'] - x['close'])**2) * math.tan(math.radians(x['sma1200_degrees']))/1200, axis=1)
df['sma1200_mrma'] = talib.SMA(np.asarray(df['sma1200_minus_range']), 60)
df['sma1200_mrinc'] = df.sma1200_mrma - df.sma1200_mrma.shift()
df['sma1200_mrdeg'] = df['sma1200_mrinc'].apply(lambda x: math.degrees(math.atan2(x, 3*60)))직각삼각형의 넓이의 이름은 minus_range이고 이값을 이동평균 한 값은 mrma로 정했습니다. 그리고 다시 mrma의 증감 값을 구하고 이 값의 각도를 다시 구했습니다. 이 값을 mrdeg로 했는데 사실 이 값은 그리 중요하지 않습니다. 딮러닝의 시그모이드(다차원의 값을 0과 1로만 표현하게 변환하는 모델) 같은 역할을 하는 값입니다. 이 값이 양수 이면 계속 상승 중인 거고 이 값이 음수이면 하락 반전한 것입니다. 즉 sma1200_degrees가 30을 넘어가면 가격이 얼마이던지 중요하지 않고 무조건 매수를 합니다. 다면 sma1200_mrdeg가 양수 일 때만 인 거죠. 그러다가 상승 에너지가 점점 약해지면 sma1200_mrdeg가 음수로 전환됩니다. 자 이젠 파도타기를 멈추고 해변으로 탈출해야 하는 시기입니다. 즉 가지고 있던 모든 비트코인을 매도하고 잠시 해변으로 나와 파도를 감상하는 타임을 가지는 거죠. ㅋㅋㅋㅋㅋ 저는 이 공식을 만들고 급락할 때도 이익을 내고 있습니다. 왜냐하면 급락도 위의 식의 반대가 되는 거죠. 급락 구간도 두 구간으로 나누고 -30 º 에서는 매수와 매도를 계속하게 했습니다. 그러다가 -40 º가 되면 급락이 시작되는 것이기에 무조건 매도합니다. 이때는 수익률이 약간 손해를 봅니다. 이유는 사실 이때가 최저가인지 아니며 지옥의 문 앞인지 저도 컴퓨터도 예측이 불가능하기 때문이죠. 이건 어떤 누구도 예측이 불가합니다. 저는 이번 하락 구간에서 -40 º가 하루를 넘기는 적도 보았습니다. 어쨌든 계속 폭락하던 값이 언제 멈출지는 이제 sma1200_mrdeg를 이용하면 쉽게 알 수 있습니다. sma1200_mrdeg 값이 점점 줄다가 양수로 변하면 무조건 매수를 시작합니다. 아주 빨리 올인을 해야 하죠 그리고 상승장을 기다립니다. 대부분은 급락 후는 바로 급등이고 일부는 급락 후에는 제가 이름 붙인 '렌딩 구간'이 발생합니다. 렌딩의 끝이 바로sma1200_mrdeg가 양수로 변하는 순간인 거죠.
3. 마치며
이번 회차에서는 추상적인 개념을 설명하다보니 여러 세계관을 왔다 갔다 했습니다. 저는 1970년대 사람이라 다른 시대를 사신 분들과 저의 어린 시절(고교 수학 시절)이 많이 다를 수 있을 것으로 생각됩니다. 물론 저도 파도타기 세계관을 경험하지는 못했습니다. 다만 어린시절 본 '폭풍 속으로'라는 영화를 상상해 보았습니다. 주인공 키아누 리부스의 명연기가 생각나는 영화입니다. 은행강도를 잡으려 강도단에 잠입한 잠입형사역인데 익스트림을 즐기는 보니(패트릭 스웨이지)에 완전히 반해버려 보니의 꿈인 가장 큰 파도를 타는 꿈을 위해서 체포를 포기합니다. 영화 마지막 장면은 폭풍속 집채만 한 파도 속으로 보니가 뛰어들고 자니(키아누 리부스)는 체포를 포기하는 장면으로 끝이 납니다. 보니가 죽었는지 살았는지는 아무도 알 수 없습니다. 비트코인 투자를 하시는 여러분들도 이미 가상의 익스트림을 하고 있다고 저는 생각합니다. 저는 여러분들이 보니 같은 사람이 아니었으면 합니다.
'python > 자동매매 프로그램' 카테고리의 다른 글
| python Bitcoin 자동 매매 프로그램(7) - 파도타기 (5) | 2021.08.11 |
|---|---|
| python Bitcoin 자동 매매 프로그램(6) - 나의 Bithum API 극복기 (1) | 2021.08.05 |
| python Bitcoin 자동 매매 프로그램(4)-Bithumb 연동 (0) | 2021.05.30 |
| python Bitcoin 자동 매매 프로그램(3)-5분 데이터와 보조지표의 연동 (0) | 2021.05.23 |
| python Bitcoin 자동 매매 프로그램(2) - 보조 지표 구하기 (0) | 2021.05.23 |